Javascript required
Skip to content Skip to sidebar Skip to footer
Home / Real Roots With Continued Fractions Lagrange

Real Roots With Continued Fractions Lagrange

Periodic Continued Fractions

A periodic continued fraction is one which "repeats" --- for example,

$$[1, 2, \overline{3, 4}] = 1 + \dfrac{1}{2 + \dfrac{1}{3 + \dfrac{1}{4 + \dfrac{1}{3 + \dfrac{1}{4 + \ddots}}}}}.$$

In general, a periodic continued fraction has the form

$$[a_0, \ldots a_m, \overline{b_1, \ldots, b_n}].$$

If n is the length of the smallest repeating part, we say that the period is n. Thus, in the example above, the period is 2.

The primary result of this section is a theorem of Lagrange which charactertizes periodic continued fractions: They correspond to irrational numbers which are roots of quadratic equations with integer coefficients. Moreover, one part of the proof will require the construction of an algorithm for computing the continued fraction expansion for a quadratic irrational --- it is different from the general continued fraction algorithm, and important in its own right.

Before I begin, I should note that this section is rather long and technical. I've tried to write out the details with care to make them easy to follow, but they are often kind of dry. You've been warned!

Definition. A quadratic irrational is an irrational number which is a root of a quadratic equation

$$a x^2 + b x + c = 0, \quad a, b, c \in \integer, \quad a \ne 0.$$

Proposition. A number is a quadratic irrational if and only if it can be written in the form $\dfrac{p + \sqrt{q}}{r}$ , where $p, q, r \in \integer$ , $r \ne 0$ , and q is positive and not a perfect square.

Proof. Suppose x is a quadratic irrational. Then x is a root of

$$a x^2 + b x + c = 0, \quad a, b, c \in \integer, a \ne 0.$$

By the quadratic formula,

$$x = \dfrac{-b \pm \sqrt{b^2 - 4 a c}}{2 a}.$$

$-b$ and $b^2 - 4 a c$ and $2 a$ are integers, and $2 a \ne 0$ , since $a \ne 0$ .

If $b^2 - 4 a c = 0$ , then $x = -\dfrac{b}{2 a}$ , which is a rational number, contrary to assumption.

If $b^2 - 4 a c < 0$ , then x is complex, again contrary to assumption.

Hence, $b^2 - 4 a c > 0$ .

Finally, if $b^2 - 4 a c$ is a perfect square, then $x = \dfrac{-b \pm \sqrt{b^2 - 4 a c}}{2 a}$ is rational. Hence, $b^2 - 4 a c$ is not a perfect square.

For the converse, suppose $x = \dfrac{p + \sqrt{q}}{r}$ , where $p, q, r \in \integer$ , $r \ne 0$ , and q is positive and not a perfect square. Then

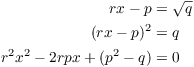
$$\eqalign{ r x - p & = \sqrt{q} \cr (r x - p)^2 & = q \cr r^2 x^2 - 2 r p x + (p^2 - q) & = 0 \cr}$$

This is a quadratic equation with integer coefficients, and $r^2 \ne 0$ since $r \ne 0$ . Therefore, x is a quadratic irrational.

I'll prove the theorem of Lagrange in two parts. First, I'll show that periodic continued fractions represent quadratic irrationals.

I need a series of lemmas; the lemmas are motivated by the informal procedure of the following example.

Example. Write $x = [5; 2, 1, 2, 2, 1, 2, 2, \ldots] = [5; 2, \overline{1, 2, 2}]$ as a quadratic irrational.

I'll write x in closed form. Let $y = [\overline{1, 2, 2}]$ . Then

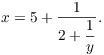
$$x = 5 + \dfrac{1}{2 + \dfrac{1}{y}}.$$

On the other hand,

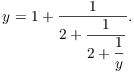
$$y = 1 + \dfrac{1}{2 + \dfrac{1}{2 + \dfrac{1}{y}}}.$$

After some simplification, I get

$$5 y^2 - 5 y - 3 = 0 \quad\hbox{so}\quad y = \dfrac{5 \pm \sqrt{37}}{10}.$$

y must be positive, so $y = \dfrac{5 + \sqrt{37}}{10}$ . Therefore,

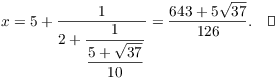
$$x = 5 + \dfrac{1}{2 + \dfrac{1}{\dfrac{5 + \sqrt{37}}{10}}} = \dfrac{643 + 5\sqrt{37}}{126}.\quad\halmos$$

The idea of the lemmas is simply to emulate the algebra I just did.

Lemma 1. If x is a quadratic irrational and $a_0$ is an integer, then $a_0 + \dfrac{1}{x}$ is a quadratic irrational.

Proof. Write $x = \dfrac{a + \sqrt{b}}{c}$ , where $a, b, c \in \integer$ , $c \ne 0$ , and b is positive and not a perfect square. Then

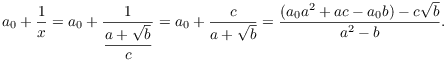
$$a_0 + \dfrac{1}{x} = a_0 + \dfrac{1}{\dfrac{a + \sqrt{b}}{c}} = a_0 + \dfrac{c}{a + \sqrt{b}} = \dfrac{(a_0 a^2 + a c - a_0 b) - c\sqrt{b}}{a^2 - b}.$$

(I've suppressed the ugly algebra involved in combining the fractions and rationalizing the denominator.) The last expression is a quadratic irrational; note that $a^2 - b \ne 0$ , because b is not a perfect square.

Lemma 2. If x is a quadratic irrational and $a_0, a_1, \ldots, a_n$ are integers, then the following expression is a quadratic irrational:

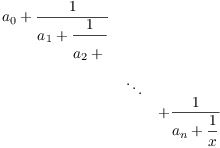
$$\matrix{a_0 + \dfrac{1}{a_1 + \dfrac{1}{a_2 + \vphantom{\dfrac{1}{a_3}}}} & & \cr & \ddots & \cr & & + \dfrac{1}{a_n + \dfrac{1}{x}} \cr}$$

Proof. I'll use induction. The case $n = 0$ was done in Lemma 1.

Suppose $n > 0$ , and suppose the result is true for $n - 1$ . nsider

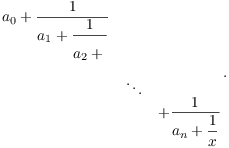
$$\matrix{a_0 + \dfrac{1}{a_1 + \dfrac{1}{a_2 + \vphantom{\dfrac{1}{a_3}}}} & & \cr & \ddots & \cr & & + \dfrac{1}{a_n + \dfrac{1}{x}} \cr}.$$

By induction, the following subfraction is a quadratic irrational:

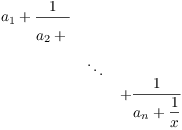
$$\matrix{a_1 + \dfrac{1}{a_2 + \vphantom{\dfrac{1}{a_3}}} & & \cr & \ddots & \cr & & + \dfrac{1}{a_n + \dfrac{1}{x}} \cr}$$

But the original fraction is just $a_0 + \dfrac{1}{(\hbox{the subfraction})}$ , so it's a quadratic irrational by Lemma 1. This completes the induction step, so the result is true for all $n \ge 0$ .

Lemma 3. Let $a_0, a_1, \ldots, a_n \in \integer$ . Let

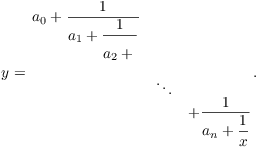
$$y = \matrix{a_0 + \dfrac{1}{a_1 + \dfrac{1}{a_2 + \vphantom{\dfrac{1}{a_3}}}} & & \cr & \ddots & \cr & & + \dfrac{1}{a_n + \dfrac{1}{x}} \cr}.$$

Then y can be written as $\dfrac{a x + b}{c x + d}$ , where $a, b, c, d \in \integer$ .

Proof. Your experience with algebra should tell you this is obvious, but I'll give the proof by induction anyway.

For $n = 0$ , I have

$$a_0 + \dfrac{1}{x} = \dfrac{a_0x + 1}{x}.$$

This has the right form.

Take $n > 0$ , and assume the result is true for $n - 1$ . Consider

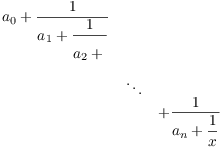
$$\matrix{a_0 + \dfrac{1}{a_1 + \dfrac{1}{a_2 + \vphantom{\dfrac{1}{a_3}}}} & & \cr & \ddots & \cr & & + \dfrac{1}{a_n + \dfrac{1}{x}} \cr}$$

By induction, for some $a, b, c, d \in \integer$ ,

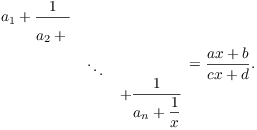
$$\matrix{a_1 + \dfrac{1}{a_2 + \vphantom{\dfrac{1}{a_3}}} & & \cr & \ddots & \cr & & + \dfrac{1}{a_n + \dfrac{1}{x}} \cr} = \dfrac{a x + b}{c x + d}.$$

The original fraction is therefore

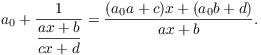
$$a_0 + \dfrac{1}{\dfrac{a x + b}{c x + d}} = \dfrac{(a_0 a + c)x + (a_0 b + d)}{a x + b}.$$

(I've suppressed some easy but ugly algebra again.) The last fraction is in the right form, so this completes the induction step. The result is therefore true for all $n \ge 0$ .

I'm ready to prove that periodic continued fractions are quadratic irrationals. First, I'll consider those that start repeating immediately. These continued fractions are purely periodic, and I'll discuss them in more detail later.

Lemma 4. If $a_0, a_1, \ldots, a_n \in \integer$ , then $x = [\overline{a_0; a_1, \ldots, a_n}]$ is a quadratic irrational.

Proof. First, x is irrational, because it is an infinite continued fraction.

By Lemma 3, for some $a, b, c, d \in \integer$ ,

$$x = [\overline{a_0; a_1, \ldots, a_n}] = [a_0; a_1, \ldots, a_n, x] = \dfrac{a x + b}{c x + d}.$$

Hence,

$$c x^2 + d x = a x + b, \quad c x^2 + (d - a) x - b = 0.$$

Therefore, x is a quadratic irrational.

In the general case, the fraction does not start repeating immediately.

Theorem. (Lagrange) Suppose $b_0, b_1, \ldots, b_m, a_0, a_1, \ldots, a_n \in \integer$ , and let

$$x = [b_0; b_1, \ldots, b_m, \overline{a_0, a_1, \ldots, a_n}].$$

Then x is a quadratic irrational.

Proof. $[\overline{a_0, a_1, \ldots, a_n}]$ is a quadratic irrational by Lemma 4. Therefore, $x = [b_0; b_1, \ldots, b_m, x]$ is a quadratic irrational by Lemma 2.

The converse states the quadratic irrationals give rise to periodic continued fractions. Before I give the proof, here's an example which shows how you can go from a quadratic equation to a periodic continued fraction (at least in this case).

Suppose x is a quadratic irrational satisfying $x^2 + x - 1 = 0$ . This gives

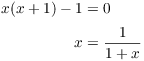
$$\eqalign{ x (x + 1) - 1 & = 0 \cr \noalign{\vskip2pt} x & = \dfrac{1}{1 + x} \cr}$$

Now substitute $x = \dfrac{1}{1 + x}$ for x in the right side:

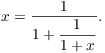
$$x = \dfrac{1}{1 + \dfrac{1}{1 + x}}.$$

Do it again:

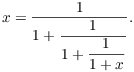
$$x = \dfrac{1}{1 + \dfrac{1}{1 + \dfrac{1}{1 + x}}}.$$

It's clear that you can keep going, and so $x = [0; \overline{1}]$ .

The proof that quadratic irrationals give rise to periodic continued fractions will come out of an algorithm for computing the continued fraction for a quadratic irrational, which is useful in its own right. First, I need to be able to write a quadratic irrational in a "standard form".

Recall that a general quadatic irrational is an expression of the form $\dfrac{a + \sqrt{b}}{c}$ , where $a, b, c \in \integer$ , $c \ne 0$ , $b > 0$ , and b is not a perfect square. In the next lemma, I'll show that a quadratic irrational can be written in a special form, which I'll need for the algorithm which follows.

Lemma. Every quadratic irrational can be written in the form $\dfrac{m + \sqrt{d}}{s}$ , where:

(a) $s \mid d - m^2$ .

(b) $m, s, d \in \integer$ .

(c) $s \ne 0$ .

(d) $d > 0$ , and d is not a perfect square.

Proof. Let $\dfrac{a + \sqrt{b}}{c}$ be a quadratic irrational, where $a, b, c \in \integer$ , $c \ne 0$ , $b > 0$ , and b is not a perfect square. Write

$$\dfrac{a + \sqrt{b}}{c} = \dfrac{a |c| + \sqrt{b c^2}}{c |c|}.$$

First,

$$b c^2 - (a |c|)^2 = b c^2 - a^2 c^2 = (b - a^2) c^2.$$

Thus, $c |c| \mid b c^2 - (a |c|)^2$ .

Obviously, $a |c|, b c^2, c |c| \in \integer$ .

Since $c \ne 0$ , I have $c |c| \ne 0$ .

Since $b > 0$ , I have $b c^2 > 0$ . Since b is not a perfect square, $b c^2$ is not a perfect square.

For example, $\dfrac{4 + \sqrt{5}}{3}$ is not in the form specified by the lemma. But I can write

$$\dfrac{4 + \sqrt{5}}{3} = \dfrac{3 \cdot 4 + \sqrt{3^2 \cdot 5}}{3 \cdot 3} = \dfrac{12 + \sqrt{45}}{9}.$$

Now $12^2 - 45 = 99$ which is divisible by 9, so the last fraction is in the correct form.

With a quadratic irrational expressed in this special form, I can construct an algorithm for computing its continued fraction. I'll compare this to the general continued fraction algorithm below.

Theorem. Let $x = \dfrac{m + \sqrt{d}}{s}$ be a quadratic irrational, where $s \mid d - m^2$ , $m, s, d \in \integer$ , $s \ne 0$ , $d > 0$ , and d is not a perfect square.

Then there are infinite sequences of integers $m_k$ , $s_k$ , and $a_k$ and an infinite sequence of irrational numbers $x_k$ defined by:

$$m_0 = m, \quad s_0 = s, \quad x_0 = x, a_0 = [x_0],$$

$$m_{k + 1} = a_k s_k - m_k \quad\hbox{for}\quad k \ge 0,$$

$$s_{k + 1} = \dfrac{d - m_{k + 1}^2}{s_k} \quad\hbox{for}\quad k \ge 0,$$

$$x_{k + 1} = \dfrac{m_{k + 1} + \sqrt{d}}{s_{k + 1}} \quad\hbox{for}\quad k \ge 0,$$

$$a_{k + 1} = [x_{k + 1}] \quad\hbox{for}\quad k \ge 0.$$

These sequences satisfy:

(a) $s_k \ne 0$ and $s_k \mid d - m_{k + 1}^2$ and $s_{k + 1} \mid d - m_{k + 1}^2$ for $k \ge 0$ .

(b) $x = [a_0, a_1, \ldots]$ .

Proof. Step 1. $m_k$ , $s_k$ , and $a_k$ are integers for $k \ge 0$ . Further, $s_k \ne 0$ and $s_k \mid d - m_{k + 1}^2$ and $s_{k + 1} \mid d - m_{k + 1}^2$ for $k \ge 0$ .

Clearly, $a_k$ is an integer for $k \ge 0$ , and $m_0$ and $s_0$ are integers by definition. I also have $s_0 = s \ne 0$ .

Now

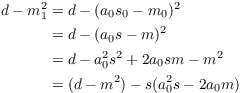
$$\eqalign{ d - m_1^2 & = d - (a_0 s_0 - m_0)^2 \cr & = d - (a_0 s - m)^2 \cr & = d - a_0^2 s^2 + 2 a_0 s m - m^2 \cr & = (d - m^2) - s (a_0^2 s - 2 a_0 m) \cr}$$

Since $s \mid d - m^2$ , it follows that $s_0 = s \mid d - m_1^2$ . This means that $s_1 = \dfrac{d - m_1^2}{s_0}$ is an integer, and I have $s_0 s_1 = d - m_1^2$ . This shows that $s_1 \mid d - m_1^2$ .

Thus, the assertions in this step are true for $k = 0$ .

Suppose the assertions hold for k. Thus, $m_k$ and $s_k$ are integers and $s_k \ne 0$ . Then $m_{k + 1} = a_k s_k - m_k$ is an integer.

If $s_{k + 1} = 0$ , then

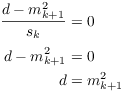
$$\eqalign{ \dfrac{d - m_{k + 1}^2}{s_k} & = 0 \cr \noalign{\vskip2pt} d - m_{k + 1}^2 & = 0 \cr d & = m_{k + 1}^2 \cr}$$

This contradicts the assumption that d is not a square. Hence, $s_{k + 1} \ne 0$ .

Next,

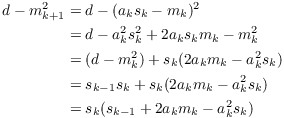
$$\eqalign{ d - m_{k + 1}^2 & = d - (a_k s_k - m_k)^2 \cr & = d - a_k^2 s_k^2 + 2 a_k s_k m_k - m_k^2 \cr & = (d - m_k^2) + s_k (2 a_k m_k - a_k^2 s_k) \cr & = s_{k - 1} s_k + s_k (2 a_k m_k - a_k^2 s_k) \cr & = s_k (s_{k - 1} + 2 a_k m_k - a_k^2 s_k) \cr}$$

This proves that $s_k \mid d - m_{k + 1}^2$ , so $s_{k + 1} = \dfrac{d - m_{k + 1}^2}{s_k}$ is an integer.

From $s_{k + 1} = \dfrac{d - m_{k + 1}^2}{s_k}$ I get $s_k s_{k + 1} = d - m_{k + 1}^2$ , so $s_{k + 1}^2 \mid d - m_{k + 1}^2$ . This establishes the assertions in Step 1 by induction.

Step 2. $x = [a_0, a_1, \ldots]$ .

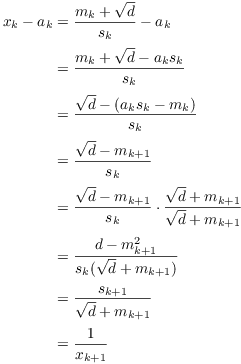
$$\eqalign{ x_k - a_k & = \dfrac{m_k + \sqrt{d}}{s_k} - a_k \cr \noalign{\vskip2pt} & = \dfrac{m_k + \sqrt{d} - a_k s_k}{s_k} \cr \noalign{\vskip2pt} & = \dfrac{\sqrt{d} - (a_k s_k - m_k)}{s_k} \cr \noalign{\vskip2pt} & = \dfrac{\sqrt{d} - m_{k + 1}}{s_k} \cr \noalign{\vskip2pt} & = \dfrac{\sqrt{d} - m_{k + 1}}{s_k} \cdot \dfrac{\sqrt{d} + m_{k + 1}}{\sqrt{d} + m_{k + 1}} \cr \noalign{\vskip2pt} & = \dfrac{d - m_{k + 1}^2}{s_k (\sqrt{d} + m_{k + 1})} \cr \noalign{\vskip2pt} & = \dfrac{s_{k + 1}}{\sqrt{d} + m_{k + 1}} \cr \noalign{\vskip2pt} & = \dfrac{1}{x_{k + 1}} \cr}$$

Hence, $x_{k + 1} = \dfrac{1}{x_k - a_k}$ . Since $a_{k + 1} = [x_{k + 1}]$ , this shows that the $a_k$ 's are the partial quotients of x.

Example. Use the quadratic irrational algorithm to compute the first 5 terms and convergents of the continued fraction for $\dfrac{2 + \sqrt{7}}{3}$ .

Note that $3 \mid 7 - 2^2$ , so the quadratic irrational is in the correct form.

The computation starts with $d = 7$ , and

$$m_0 = 2, \quad s_0 = 3, \quad x_0 = \dfrac{2 + \sqrt{7}}{3} \approx 1.54858 \ldots, \quad a_0 = 1.$$

Then

$$m_1 = a_0 s_0 - m_0 = 1 \cdot 3 - 2 = 1.$$

$$s_1 = \dfrac{d - m_1^2}{s_0} = \dfrac{7 - 1^2}{3} = 2.$$

$$x_1 = \dfrac{m_1 + \sqrt{d}}{s_1} = \dfrac{1 + \sqrt{7}}{2} = 1.82287 \ldots.$$

$$a_1 = [x_1] = 1.$$

Continuing in this way, I obtain:

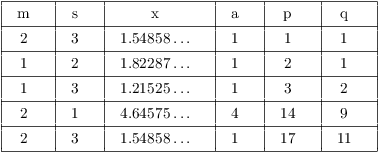
$$\vbox{\offinterlineskip \halign{& \vrule # & \strut \hfil \quad # \quad \hfil \cr \noalign{\hrule} height2pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr & m & & s & & x & & a & & p & & q & \cr height2pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr & 2 & & 3 & & $1.54858 \ldots$ & & 1 & & 1 & & 1 & \cr height2pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr & 1 & & 2 & & $1.82287 \ldots$ & & 1 & & 2 & & 1 & \cr height2pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr & 1 & & 3 & & $1.21525 \ldots$ & & 1 & & 3 & & 2 & \cr height2pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr & 2 & & 1 & & $4.64575 \ldots$ & & 4 & & 14 & & 9 & \cr height2pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr & 2 & & 3 & & $1.54858 \ldots$ & & 1 & & 17 & & 11 & \cr height2pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} }} $$

It is interesting to compare this algorithm to the general continued fraction algorithm:

$$x_0 = x, \quad a_0 = [x_0],$$

$$x_k = \dfrac{1}{x_{k - 1} - a_{k - 1}}, \quad a_k = [x_k] \quad\hbox{for}\quad k \ge 1.$$

If I apply the general algorithm to $\dfrac{2 + \sqrt{7}}{3}$ , I get

$$[1, 1, 1, 4, 1, 1, 1, 4, 1, 1, 1, 4, 1, 1, 1, 4, 1, 1, 1, 4, 1, 1, 1, 4, 1, 1, 1, 5, 1, 6, \ldots]$$

I used a typical computer program to do the computation; you may get a slightly different result depending on what software you use. Notice that the partial quotients (which should be periodic) have started to be incorrect.

The quadratic irrational algorithm gives

$$[1, 1, 1, 4, 1, 1, 1, 4, 1, 1, 1, 4, 1, 1, 1, 4, 1, 1, 1, 4, 1, 1, 1, 4, 1, 1, 1, 4, 1, 1, \ldots]$$

The general algorithm is unstable because the division $\dfrac{1}{x_{k - 1} - a_{k - 1}}$ magnifies the round-off errors which will occur in the floating-point computations. The quadratic irrational algorithm is more stable, and continues to produce the correct periodic partial quotients.

I will digress mometarily to prove an easy observation about the quadratic irrational algorithm. It's not needed for Lagrange's theorem, but I'll need it later in discussing continued fractions for irrationals of the form $\sqrt{d}$ .

Proposition. Let $x = \dfrac{m + \sqrt{d}}{s}$ be a quadratic irrational, where $s \mid d - m^2$ , $m, s, d \in \integer$ , $s \ne 0$ , $d > 0$ , and d is not a perfect square. Suppose the quadratic irrational algorithm is applied to x, yielding sequences $m_k$ , $s_k$ , and $x_k$ .

Then $x_i = x_j$ if and only if $(m_i, s_i) = (m_j, s_j)$ .

Proof. If $(m_i, s_i) = (m_j, s_j)$ , then

$$x_i = \dfrac{m_i + \sqrt{d}}{s_i} = \dfrac{m_j + \sqrt{d}}{s_j} = x_j.$$

Conversely, suppose $x_i = x_j$ . Then

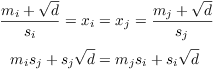
$$\eqalign{ \dfrac{m_i + \sqrt{d}}{s_i} = x_i & = x_j = \dfrac{m_j + \sqrt{d}}{s_j} \cr \noalign{\vskip2pt} m_i s_j + s_j \sqrt{d} & = m_j s_i + s_i \sqrt{d} \cr}$$

Equating rational and irrational parts on the two sides, I have

$$m_i s_j = m_j s_i \quad\hbox{and}\quad s_j = s_i.$$

Since $s_j = s_i \ne 0$ , I have $m_i = m_j$ . Thus, $(m_i, s_i) = (m_j, s_j)$ .

As an example, here are the first 7 values of $m_k$ , $s_k$ , and $x_k$ for $\dfrac{5 + \sqrt{11}}{7}$ . Compare the values of $x_k$ and $(m_k, x_k)$ :

$$\vbox{\offinterlineskip \halign{& \vrule # & \strut \hfil \quad # \quad \hfil \cr \noalign{\hrule} height2pt & \omit & & \omit & & \omit & \cr & m & & s & & x & \cr height2pt & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2pt & \omit & & \omit & & \omit & \cr & 5 & & 7 & & $1.18808 \ldots$ & \cr height2pt & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2pt & \omit & & \omit & & \omit & \cr & 2 & & 1 & & $5.31662 \ldots$ & \cr height2pt & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2pt & \omit & & \omit & & \omit & \cr & 3 & & 2 & & $3.15831 \ldots$ & \cr height2pt & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2pt & \omit & & \omit & & \omit & \cr & 3 & & 1 & & $6.31662 \ldots$ & \cr height2pt & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2pt & \omit & & \omit & & \omit & \cr & 3 & & 2 & & $3.15831 \ldots$ & \cr height2pt & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2pt & \omit & & \omit & & \omit & \cr & 3 & & 1 & & $6.31662 \ldots$ & \cr height2pt & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2pt & \omit & & \omit & & \omit & \cr & 3 & & 2 & & $3.15831 \ldots$ & \cr height2pt & \omit & & \omit & & \omit & \cr \noalign{\hrule} }} $$

We continue with our discussion of Lagrange's theorem. Next, I need to derive some results on conjugates of quadratic irrationals.

Definition. Let $a, b, c \in \integer$ , where $c \ne 0$ . Let $d \in \integer^+$ , and suppose d is not a perfect square. The conjugate of $\dfrac{a + b \sqrt{d}}{c}$ is

$$\overline{\dfrac{a + b \sqrt{d}}{c}} = \dfrac{a - b \sqrt{d}}{c}.$$

Note that if $b = 0$ , then I get the number rational number $\dfrac{a}{c}$ , whose conjugate is itself.

The properties that follow are sufficiently formal that "$\sqrt{d}$ " could be replaced with "x". Note that in all the expressions the "radical part" is the same ($\sqrt{u}$ ). I've switched from "$\sqrt{d}$ " to "$\sqrt{u}$ " for readability, since I need two quadratic irrationals for each property. The proof of this proposition is just tedious basic algebra, so you could skip it, or just work out some of the parts yourself.

Proposition. Let

$$x = \dfrac{a + b \sqrt{u}}{c} \quad\hbox{and}\quad y = \dfrac{d + e \sqrt{u}}{f}.$$

Assume that $a, b, c, d, e, f \in \integer$ , $c, f \ne 0$ , $u \in \integer^+$ , and u is not a perfect square.

(a) $\overline{x + y} = \overline{x} + \overline{y}$ .

(b) $\overline{x \cdot y} = \overline{x} \cdot \overline{y}$ .

(c) $\overline{\dfrac{x}{y}} = \dfrac{\overline{x}}{\overline{y}}$ .

Proof. (a)

$$\overline{\left(\dfrac{a + b \sqrt{u}}{c} + \dfrac{d + e \sqrt{u}}{f}\right)} = \overline{\dfrac{(a f + c d) + (b f + c e) \sqrt{u}}{c f}} = \dfrac{(a f + c d) - (b f + c e) \sqrt{u}}{c f}.$$

$$\overline{\dfrac{a + b \sqrt{u}}{c}} + \overline{\dfrac{d + e \sqrt{u}}{f}} = \dfrac{a - b \sqrt{u}}{c} + \dfrac{d - e \sqrt{u}}{f} = \dfrac{(a f + c d) - (b f + c e) \sqrt{u}}{c f}.$$

(b)

$$\overline{\left(\dfrac{a + b \sqrt{u}}{c} \cdot \dfrac{d + e \sqrt{u}}{f}\right)} = \overline{\dfrac{(a d + b e u) + (a e + b d) \sqrt{u}}{c f}} = \dfrac{(a d + b e u) - (a e + b d) \sqrt{u}}{c f}.$$

$$\overline{\dfrac{a + b \sqrt{u}}{c}} \cdot \overline{\dfrac{d + e \sqrt{u}}{f}} = \dfrac{a - b \sqrt{u}}{c} \cdot \dfrac{d - e \sqrt{u}}{f} = \dfrac{(a d + b e u) - (a e + b d) \sqrt{u}}{c f}.$$

(c)

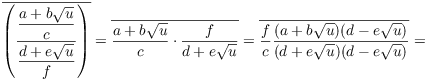
$$\overline{\left(\dfrac{\dfrac{a + b \sqrt{u}}{c}}{\dfrac{d + e \sqrt{u}}{f}}\right)} = \overline{\dfrac{a + b \sqrt{u}}{c} \cdot \dfrac{f}{d + e \sqrt{u}}} = \overline{\dfrac{f}{c} \dfrac{(a + b \sqrt{u})(d - e \sqrt{u})}{(d + e \sqrt{u}) (d - e \sqrt{u})}} =$$

$$\overline{\dfrac{f}{c} \dfrac{(a + b \sqrt{u}) (d - e \sqrt{u})}{d^2 - e^2 u}} = \dfrac{f}{c (d^2 - e^2 u)} \overline{(a + b \sqrt{u}) (d - e \sqrt{u})} = \dfrac{f}{c (d^2 - e^2 u)} \overline{a + b \sqrt{u}} \cdot \overline{d - e \sqrt{u}} =$$

$$\dfrac{f}{c (d^2 - e^2 u)} (a - b \sqrt{u}) (d + e \sqrt{u}) = \dfrac{f}{c} \dfrac{(a - b \sqrt{u}) (d + e \sqrt{u})}{(d - e \sqrt{u}) (d + e \sqrt{u})} = \dfrac{f}{c} \dfrac{a - b \sqrt{u}}{d - e \sqrt{u}} =$$

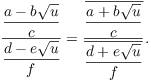
$$\dfrac{\dfrac{a - b \sqrt{u}}{c}}{\dfrac{d - e \sqrt{u}}{f}} = \dfrac{\overline{\dfrac{a + b \sqrt{u}}{c}}}{\overline{\dfrac{d + e \sqrt{u}}{f}}}.$$

The fourth and fifth equalities used (b).

Now I can prove the other half of Lagrange's theorem.

Theorem. (Lagrange) The continued fraction for a quadratic irrational is periodic.

Proof. I will use the notation of the quadratic irrational continued fraction algorithm. Thus, I assume $x = \dfrac{m + \sqrt{d}}{s}$ with $m, s \in \integer$ , $s \ne 0$ , $d \in \integer^+$ , d is not a perfect square, and $s \mid d - m^2$ . Then the sequences $\{m_n\}$ , $\{s_n\}$ , $\{x_n\}$ , and $\{a_n\}$ are defined recursively by the algorithm.

The idea is to show that for large values of n, the $s_n$ 's and $m_n$ 's only assume only finitely many values. This will imply that the same is true for the $x_n$ 's, and hence that the continued fraction for x is periodic.

The first and longest step sets things up by showing that the $s_n$ 's are eventually positive.

Step 1. $s_n > 0$ for sufficiently large n.

Recall that if x is an irrational number, the general continued fraction algorithm is

$$x_0 = x, \quad a_0 = [x_0],$$

$$x_n = \dfrac{x_{n - 1} - a_{n - 1}}, \quad a_n = [x_n] \quad\hbox{for}\quad n \ge 1.$$

I showed that

$$x_0 = [a_0, a_1, \ldots a_{n - 1}, x_n].$$

The $n^{\rm th}$ convergent of this continued fraction is equal to $x = x_0$ (since this is a finite continued fraction), and the convergents algorithm say that the $n^{\rm th}$ convergent is $\dfrac{p_{n - 1} x_n + p_{n - 2}}{q_{n - 1} x_n + q_{xn - 2}}$ . Thus,

$$x_0 = \dfrac{p_{n - 1} x_n + p_{n - 2}}{q_{n - 1} x_n + q_{n - 2}}.$$

In our situation, $x_0$ is a quadratic irrational $\dfrac{a + \sqrt{d}}{b}$ . But the quadratic irrational continued fraction algorithm shows that $x_n$ is a quadratic irrational of the form $\dfrac{e + \sqrt{d}}{f}$ --- that is, $x_0$ and $x_n$ are quadratic irrationals with the same radical term $\sqrt{d}$ . Therefore, I may apply the properties of conjugates I derived:

$$\overline{x_0} = \overline{\left(\dfrac{p_{n - 1} x_n + p_{n - 2}}{q_{n - 1} x_n + q_{n - 2}}\right)} = \dfrac{\overline{p_{n - 1} x_n + p_{n - 2}}}{\overline{q_{n - 1} x_n + q_{n - 2}}} = \dfrac{\overline{p_{n - 1} x_n} + \overline{p_{n - 2}}}{\overline{q_{n - 1} x_n} + \overline{q_{n - 2}}} = \dfrac{\overline{p_{n - 1}}\ \overline{x_n} + \overline{p_{n - 2}}}{\overline{q_{n - 1}}\ \overline{x_n} + \overline{q_{n - 2}}} = \dfrac{p_{n - 1} \overline{x_n} + p_{n - 2}}{q_{n - 1} \overline{x_n} + q_{n - 2}}.$$

Solve for $\overline{x_n}$ :

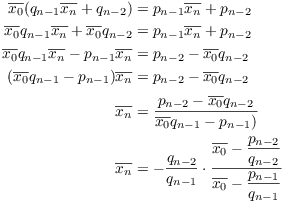
$$\eqalign{ \overline{x_0} (q_{n - 1} \overline{x_n} + q_{n - 2}) & = p_{n - 1} \overline{x_n} + p_{n - 2} \cr \overline{x_0} q_{n - 1} \overline{x_n} + \overline{x_0} q_{n - 2} & = p_{n - 1} \overline{x_n} + p_{n - 2} \cr \overline{x_0} q_{n - 1} \overline{x_n} - p_{n - 1} \overline{x_n} & = p_{n - 2} - \overline{x_0} q_{n - 2} \cr (\overline{x_0} q_{n - 1} - p_{n - 1}) \overline{x_n} & = p_{n - 2} - \overline{x_0} q_{n - 2} \cr \noalign{\vskip2pt} \overline{x_n} & = \dfrac{p_{n - 2} - \overline{x_0} q_{n - 2}}{\overline{x_0} q_{n - 1} - p_{n - 1})} \cr \overline{x_n} & = -\dfrac{q_{n - 2}}{q_{n - 1}} \cdot \dfrac{\overline{x_0} - \dfrac{p_{n - 2}}{q_{n - 2}}}{\overline{x_0} - \dfrac{p_{n - 1}}{q_{n - 1}}} \cr}$$

As $n \to \infty$ the convergents $\dfrac{p_{n - 2}}{q_{n - 2}}$ and $\dfrac{p_{n - 1}}{q_{n - 1}}$ both approach $x_0$ , and $x_0 \ne \overline{x_0}$ . It follows that

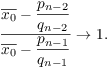
$$\dfrac{\overline{x_0} - \dfrac{p_{n - 2}}{q_{n - 2}}}{\overline{x_0} - \dfrac{p_{n - 1}}{q_{n - 1}}} \to 1.$$

Moreover, for large n I have $q_{n - 2}, q_{n - 1} > 0$ . So for large n,

$$\overline{x_n} \approx -\dfrac{q_{n - 2}}{q_{n - 1}} < 0.$$

Since $x_n > 0$ , I have $x_n - \overline{x_n} > 0$ for large n.

Now using the notation of the quadratic irrational continued fraction algorithm,

$$x_n = \dfrac{m_n + \sqrt{d}}{s_n} \quad\hbox{and}\quad \overline{x_n} = \dfrac{m_n - \sqrt{d}}{s_n}.$$

So

$$x_n - \overline{x_n} = \dfrac{2 \sqrt{d}}{s_n}.$$

Thus, for sufficiently large n,

$$\dfrac{2 \sqrt{d}}{s_n} > 0, \quad\hbox{so}\quad s_n > 0.$$

Step 2. $s_n$ assumes only finitely many values For sufficiently large n.

The quadratic irrational algorithm gives

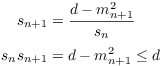
$$\eqalign{ s_{n + 1} & = \dfrac{d - m_{n + 1}^2}{s_n} \cr \noalign{\vskip2pt} s_n s_{n + 1} & = d - m_{n + 1}^2 \le d \cr}$$

For large n, I know $s_{n + 1}$ is a positive integer, so $s_{n + 1} \ge 1$ . Hence,

$$d \ge s_n s_{n + 1} \ge s_n.$$

For sufficiently large n I know $s_n$ is positive. Therefore, $s_n$ assumes only finitely many values (between 0 and d) for sufficiently large n.

Step 3. $m_n$ assumes only finitely many values For sufficiently large n.

For sufficiently large n I have $s_n s_{n + 1} > 0$ . Hence,

$$m_{n + 1}^2 < m_{n + 1}^2 + s_n s_{n + 1} = d.$$

Thus, $0 \le |m_{n + 1}| < \sqrt{d}$ . So $m_{n + 1}$ assumes only finitely many values for sufficiently large n (and the same is true for $m_n$ ).

Step 4. The continued fraction for x is periodic.

Steps 3 and 4 show that for sufficiently large n the pairs $(m_n, s_n)$ assume only finitely many values. Therefore, there are distinct integers i and j --- say $i < j$ --- such that $(m_i, s_i) = (m_j, s_j)$ . Then

$$x_i = \dfrac{m_i + \sqrt{d}}{s_i} = \dfrac{m_j + \sqrt{d}}{s_j} = x_j.$$

Thus,

$$a_i = [x_i] = [x_j] = a_j.$$

Moreover, the quadratic irrational algorithm shows that if $(m_i, s_i) = (m_j, s_j)$ , then $(m_{i + 1}, s_{i + 1}) = (m_{j + 1}, s_{j + 1})$ , and successive pairs continue to be equal. So

$$x = x_0 = [a_o, a_1, \ldots a_{i - 1}, \overline{a_i, a_{i + 1}, \ldots, a_{j - 1}}].$$

This proves that the continued fraction for x is periodic.

Contact information

Bruce Ikenaga's Home Page

Copyright 2019 by Bruce Ikenaga

logicegooks.blogspot.com

Source: https://sites.millersville.edu/bikenaga/number-theory/periodic-continued-fractions/periodic-continued-fractions.html